Coulomb’s law definition in physics is explained by the concept of electric charge and electric force. According to Electricity, moving electric charges experience force when kept in a magnetic field.
Here the charge is in the form of matter which may be a positive charge or negative charge. The positive charge is the composition of protons and negative charge contains electrons. When protons or electrons move in the electric field they produce an electric current. Here are some properties of the electric charge.
Properties of Electric Charge
- The Law of conserving charge states that charge or energy is neither created nor destroyed. It is in the form of charged objects that influence nearby objects (charged or uncharged).
- A charge is a Scalar quantity and its units are Coulombs.
- The movement of charges is free through the conductors and does not conduct through the insulator.
- When the size of charged objects is small than the distance between them, they are called the point of charges.
- Charges can be added together having a magnitude with no direction.
Electric Force as Vector Quantity
These five properties of electric charge leading to a phenomenon called static electricity. An example of static electricity can be defined as follows. If two insulator materials are rubbed with each other, the materials gain equal and opposite charges. This results in the formation of electric force between the objects.
But the fact is, this force is a vector quantity having two parameters magnitude and direction. The question is how to determine the direction of the electrical force?
The probable answer can be found from the Coulombs law. This law uses two forces which are opposite in nature. They are attractive and repulsive force. So, let’s discuss the difference between attractive force and repulsive force.
The attractive force is often related to Newton’s Law of Gravity and is represented mathematically as
F = Gm1m2/d2
Here ‘F‘ is the attractive force
‘m1‘ and ‘m2‘ is mass of the bodies
‘d‘ is the distance between the bodies in meters
‘G‘ is universal gravitational constant which is equal to 6.67×10-11 Nm2/kg2
This equation states that an attractive force forms between two different bodies with mass and this force are directly proportional to the mass of the two bodies and inversely proportional to the square of the distance between them. Whereas repulsive force pushes back the bodies having the same quantity of mass.
What is Coulomb’s Law?
Coulomb’s law (also known as Coulomb’s inverse-square law) and electric field in electricity signify the importance of point of charges.
It was invented by Charles Augustin de Coulomb in the year 1785. He observed that an electric force exists around different charges.
Initially, the charges are considered to be at rest condition and the force between the charges is known as electrostatic force.
Definition of Coulombs Law
- Coulomb law defines that the magnitude of force existing between the two-point charges varies inversely as the square of the distance between the two charges.
- The magnitude of the force was directly proportional to the multiply of charges and also acts on the area joined by the two charges.
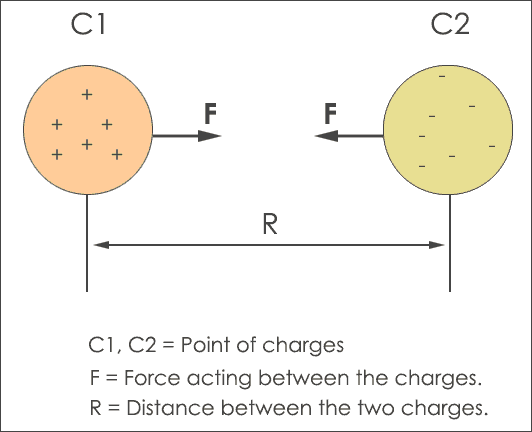
To explain the importance of the phenomenon of an attractive and repulsive force, different formulas and equations are used for derivation of coulombs law. From the above figure, the C1 object has a positive charge (protons) and the C2 object has a negative charge (electrons). The distance between the two charges C1 and C2 is ‘R‘.
In simple words, if two charges C1 and C2 are separated by distance ‘R‘ they produce electrostatic force. The amount of charge on both of the charged objects reflect the strength of the repulsive force. The more charged the object is, the more the repulsive force.
When you decrease the distance ‘R‘ the massive force increases between the two charges. In some scenarios, the charges C1, C2 are represented as q1 and q2 but this notation is not mandatory. In this tutorial, the number of charges is denoted with C1 and C2.
Gauss’s law Relation to Coulombs law
To derive Coulomb’s law from Gauss law with some assumptions. The assumption is the field produced from the electric charge is spherically symmetric in nature.
Another assumption to prove it is true is, the charge is stationary and nearly true if the charge is in the movable condition.
But the fact is the Coulombs law cannot be related to Gauss’s law and doesn’t show any details for the extent to which the Electric field rotates around coordinate axes. For stationary charges, the field is radial with no movement.
The derivation of Coulomb’s law from Gauss law is derived as follows.
By taking the spherical surface ‘S‘ with radius ‘r‘ of electric field ‘E‘ for a charge ‘C‘ which is represented as
∮ E.dA = C / ε0
As the area of the sphere is 4πr2 and integrand is a constant, the above equation can be rewritten as
(4πr2 )E(r^) = C / ε0
Where is present in radial position and we can derive the coulombs law from this equation.
E(r^) = C. /4π ε0. r2
This equation relates the electric field and inverse square law which depends on coulombs law on gauss law.
Units, Formulas and Equations
The formula or equation for coulombs law can be derived from Newton’s Law of Gravity discussed above.
The equation is similar to Newton’s Law of Gravity and is given by the formula
F= Z. |C1.C2|/ R2 – Equation 1
Where,
‘F‘ represents the net force generated between the two charges
‘Z‘ is the Coulomb Constant or electrostatic constant which is equal to 9×109 N m2 C−2
‘C1 and C2‘ represents the magnitude of charges (quantity)
‘R‘ is the distance between the two charges
From the above equation 1, the force ‘F‘ can be written as follows.
F α C1.C2 – Equation 2
Or F α 1/R2
Note: If the magnitude of charges is opposite then Force is negative in nature and if the magnitude is the same the force is positive.
The importance of coulombs law is explained in two forms i.e. scalar and vector.
The scalar form is used when it is necessary to calculate the magnitude of force (but not direction) and the vector form of coulomb law tells that, the electrostatic force ‘F1‘ happened by a charge C1 at position vector R1 and also the force ‘F2‘ experienced by nearby charge C2 at position vector R2 in a vacuum is given by

F1 = C1.C2 (R1-R2) /4πε0.|R1-R2|3
Since the charges C1, C2 are of the same sign there exists repulsive force between them.
The force for charge C1 due to due to charge C2 is F12 and force for charge C2 due to charge C1 is F21. The vector calculation for the positions is given by the equation
R21 = R2 – R1 (for F21) and R12 = R1– R2 (for F12)
The vector direction is given from position R1 to R2 and R2 to R1 is given by R^12 or R^21
Now the vector form of coulombs law is given by
F21 = C1×C2× R^21 /4πε0×R221
The force F21 and F12 are opposite in nature hence F12 = -F21. This is how the repulsive force is calculated and shows that coulombs law satisfies Newton’s third law, i.e. every action has an equal and opposite reaction.
The relation between Ampere and Coulomb
Ampere is the unit of electric current and measured in Amperes. Whereas coulomb is the SI unit of electrical charge. The difference between ampere and coulomb is ampere is used to measure charge which is flowing and coulomb is used to measure static charge.
The relation between ampere and coulomb is when one ampere of current flows across a conductor it is equal to the flow of one coulomb of charge through the conductor in the one-second interval.
Hence the definition of a coulomb is Ampere-Second which refers the charge to electric current.
Applications
Here are some of the applications of coulombs law that are universally used.
- In static charge analysis for testing capacitive modules such as electric fuses and electromagnetic transmission lines. You can also measure electric fields, electric force, and electric charge density of the capacitor.
- For grounding and protecting the electronic components from electrostatic discharge (ESD).
- To find out the distance between the charged or uncharged particles.
Drawbacks
Here are limitations of Coulombs Law which cannot be applied to certain applications. It has 3 major drawbacks.
- This law is applicable only if charges are in the static (not moving) state.
- It is justifiable only when the molecules (solvent type) between the different particles are bigger than the existing charges.
- This law is not valid for charges present in an uneven shape.
Coulombs Law Examples
To check the understanding of Coulombs Law, you can try out this example problem with solutions.
After this exercise, you will be able to do calculations on the magnitude of the force, net force, and distance between charges.
- Two-point of charges, one with 2 coulombs of charge and another with 3 coulombs of charge are kept at 2 meters. How to find the magnitude of the force between the two charges.
Solution: From the above given information, C1 = 2, C2 = 2,
R = 2 meters, Z = 9×109, Force =?
Formula to calculate repulsive force:
F= Z. |C1.C2|/ R2
Now substitute the given values in the above formula.
F = (9×109 N * m2 /C2) * (2C) * (2C) / (2m)2
Therefore the repulsive force between 2 charges is F = 9 * 109 N
- Two magnets attract each other are charged with 5 micro Coulomb and 10 micro Coulomb. The force acting on both the charges is 0.05 Newton. Find out the distance between the two magnets.
Solution: From the given data, C1 = 5×10-6C, C2 = 10×10-6C,
Z = 9×109, F = 0.05N, R =?
From the Coulombs formula, F= Z. |C1.C2|/ R2
R2 = Z. C1.C2/F
![]()
Hence, the distance between the two charges is 0.67 meters
Conclusion
The definition of coulombs law in physics explains the bonding force between the electrostatic charges and identifies the direction of the electric field for the charges.