In the previous tutorial, we had discussed the applications of current, voltage, and importance of Coulomb’s law in electricity. But, without ohms law the operation of an electric circuit becomes incomplete.
To fulfill this, Ohms Law is also involved. A German physicist Georg Simon Ohm discovered the ohms law and found the relationship between current, voltage and resistance.
In this tutorial, you will know how to apply ohms law to different applications of electrical and electronics engineering.
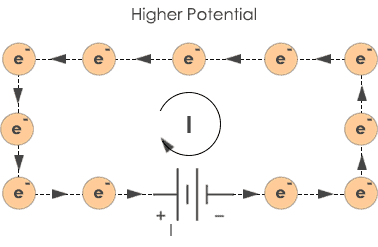
As you know, Electric current flows in the form of charged electrons. In other words, less flow of electrons means high resistance is present in the circuit. And, the high flow of electrons means low resistance is present.
Electron current is the number of electrons moving per second. However, for practical applications, we need less amount of electron charge. To simplify, two measuring units known as Ampere and Coulomb have been used.
The coulomb indicated by ‘Q’ expresses an adequate amount of electric charge.
Electric Charge is equal to 6 million electrons multiplied by 1 million electrons. This resultant charge is again multiplied by one million electrons.
The Ampere represented by ‘A’ is the strength of unit current or the number of electrons traveling per second, in this case, one coulomb per second.
An Ampere is too large for some of the applications. So, it is again divided into subparts known as milli-ampere (mA), and the micro-ampere (µA).
1 A = 1000 mA = 1,000,000 µA 1 mA = 1/1000 A = 1000 µA
Now let us discuss resistance. Since the composition of various materials is different, some materials offer high opposition to the flow of electrons than other metals. This electrical phenomenon is known as resistance.
Now, if we apply driving force or Electromagnetic force (E.M.F) across a conductor, a great number of electrons will flow rapidly. This proves that resistance of the conductor is low.
On the other hand, applying same E.M.F to an insulator will produce fewer electrons. Hence, the resistance of an insulator is high.
The resistance is expressed in Ohms and denoted by the Greek capital letter ‘Ω’. The unit of E.M.F is the Volt. One Volt is the driving force necessary force required to produce a current strength of 1A in a circuit having a resistance of 1 Ω.
The electric current is a measuring instrument called Ammeter and electrical resistance is measured using Ohm meter.
How Ohm’s Law work?
Ohm’s law relates the electrical quantities such as current, voltage, power and resistance. To know the practical use of the ohms law here is an example.
Connect a wire of certain resistance, in series with 1.5V battery source and assume that ammeter indicates a current of 0.2A. Now, if we increase the voltage to 3V, the current meter will show more current reading, say, 0.4A.
This states that by keeping the resistance as constant and increasing the voltage, the current will be doubled. By repeating this process of increasing and decreasing voltage by keeping the resistance unchanged the voltage will be proportional to the current.
A similar thing happens if we change the length of the conductor wire, keeping the applied voltage as constant.
If we change the length of wire to shorter or longer, it has some effect due to the resistance of the wire.
For example, by applying constant E.M.F of 1.5V and the length of wire is 2m, the current drawn is 0.3A.
Now, if we change the length of the wire to 1m, the current will be lesser 0.1 (but not 0.3) because of less distance to cover and less resistance to overcome.
Ohm’s Law Theory
When you take a metallic conductor and flow some current through it, the potential difference between the two ends of a conductor is constant.
Definition of Ohms Law
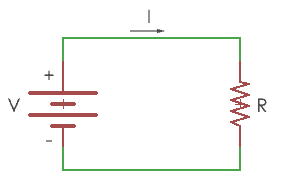Ohms law states that “the current flowing through an electrical circuit will change when a voltage is applied, but the resistance is inversely proportional to the resistance of the conductor material”.
The formula of ohms law is represented by the equation
V=IR
‘V’ is the potential drop(voltage) across the resistor.
‘I’ is the current flowing in the circuit through the resistor
‘R’ is the resistance value of resistor represented in ohms.
The above equation, I=V/R depicts the following facts.
- Current alters with the applied input voltage
If the resistance of the conductor is kept constant, the voltage will increase with an increase in current and the voltage will decrease with a decrease in current.
- Current and resistance are inverse to each other
Now keep voltage in the circuit as a constant parameter, If you change the resistance, the current will also vary.
For suppose, if the resistance is increased, the current in the circuit is decreased and if the resistance is decreased the current will increase.
- Voltage and Current relation
The relation between voltage and current is linear. i.e. with larger voltage, the current will be higher and lower current for smaller voltage.
Ohms Law Analogy
The relationship between voltage, current, and resistance can be known by finding the third quantity from the known two values.
The two known values may be either voltage, current or resistance.
Calculation of Ohms Law
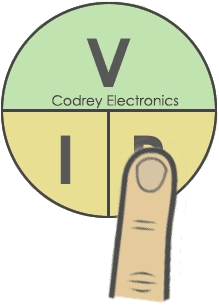
Ohm’s law can be represented in three forms. To understand simply, ohms law circle or ohms law Triangle is used in electrical circuits to find out the third quantity of the two other quantities.
The circle or triangle method is used for memorizing the ohms law.
Here I am using ohms law circle to find out voltage, current, and resistance.
- To calculate the Voltage (V), round of the voltage (V) as shown below. The current and resistance are related.
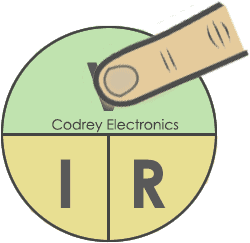
- To calculate the Current (Amperes), round of the Current(I) as shown below. This will be the current flowing in the circuit.
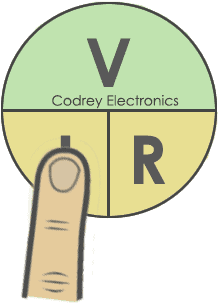
- Similarly, to find out the resistance (ohms), round of the resistance(R), you will get the resistance of the conductor.
By combining voltage, current, and resistance we can get a common relationship to draw the ohms law graph.
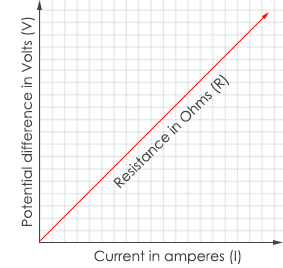
From the graph, if the current in an electrical circuit increases voltage increases linearly and vice versa.
To make the relation easier Ohms law Table is given for quick reference.
| Ohms Law | Known Values | Relationship 1 | Relationship 2 |
|---|---|---|---|
| V=IR | Current and Resistance | Voltage is directly proportional to current | Voltage is directly proportional to resistance |
| I=V/R | Voltage and Resistance | Current is inversely proportional to resistance | Current is directly proportional to Voltage |
| R=V/I | Voltage and current | Resistance is directly proportional to voltage | Resistance is inversely proportional to current |
Now, let us know how to use ohms law formulas in a practical way.
Examples of Ohm’s Law
1. Finding the current in a circuit
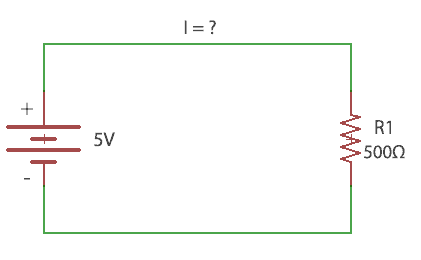Given: Voltage=5V , Resistance=500Ω, I=?
Formula:
I=V/R = 5/500= 0.01A.
So, by applying 5V potential a current of 0.01A flows through the 500 ohms resistor.
2. Finding the voltage in a circuit
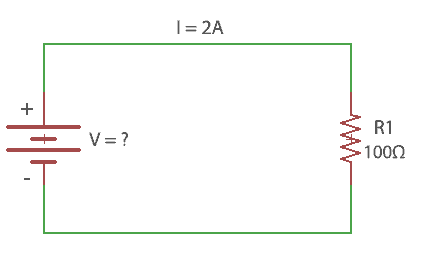Given: Resistance=100Ω, I=2A, Voltage =?
Formula:
V=IR = 2*100=200V
So, the battery voltage for the circuit is 200V.
3. Finding the resistance in a circuit
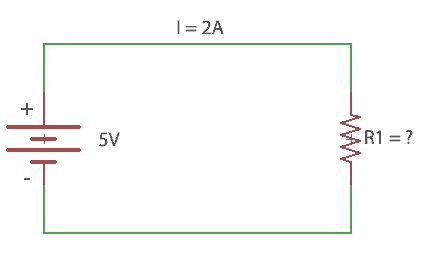Given: I=2A, Voltage = 5V, Resistance =?
Formula:
R=V/I = 5/2=2.5Ω
So, a resistance of 2.5 ohms has to be connected in series with the battery source.
Practical applications of Ohm’s Law
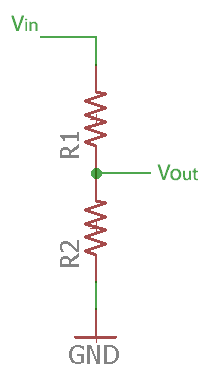
1. Power Supply design (as voltage divider)
Ohms law is useful in designing power supplies for the electronic circuits. Voltage dividers decide the regulated output for proper function of the circuit. This is achieved by choosing correct resistance using the ohms law.
2. Analog sensors
Some types of sensors gives current reading as output. For example, radar sensor gives a current output of 4-20mA.
This current output should be converted to a voltage using resistance equation. The obtained analog voltage is then processed through ADC (Analog to digital converter).
3. Speed Control
Ohms law is extensively used in speed controlling applications. It is used in potentiometer also known as “POT”. The knob resistance is varied slowly, which increases the voltage and rotates the motor or fan.
4. Simplification of circuits
It is also used in the reduction of complex electrical circuits using Kirchhoff’s Voltage Law and Kirchhoff’s Current law equation. A series and parallel circuits can be realised simply using ohms law.
Conclusion
It is important in real life to find out the current and voltages for any application. A small deviation in the output load may burn or damage the circuit. To avoid this, it is required to apply the principles of ohms law and build a valid electronic system.
